Algorithm Analysis
In this section, we study algorithm analysis and Big O notation.
Algorithm Efficiency
The efficient use of resources is one of the characteristics that determines the quality of software, such as CPU time and memory usage.The "goodness" of an algorithm is to measure how fast it executes.
Use seven functions to evaluate algorithm's running time (time complexity)
1. Constant Function
f(n) = c
For any n, f(n) is equal to a constant.
It doesn’t matter what the value of n is.
f(n) = 1
Example:
int [] myArray = new int[250000];
int sum = myArray[0] + myArray[5690];
int sum = myArray[0] + myArray[5690];
2. Linear Function
f(n) = n
Given an input n, f(n) is equal to n.
Examples:
Use a single loop to process the entire array with n elements.
int sum = 0;
for (int i = 0; i < myArray.length; i++) {
sum += myArray[i];
}
for (int i = 0; i < myArray.length; i++) {
sum += myArray[i];
}
Sequential search
Find the largest value or the smallest value in the array
3. Quadratic Function
f(n) = n2
Given an input n, f(n) is equal to the product of n.
Examples:
Nested loop: inner loop is a linear function, the outer loop is a linear function, the algorithm is n * n = n2 function.
Selection sort, bubble sort, insertion sort.
Nested loop where the 1st iteration of the inner loop uses one operation, the 2nd uses 2 operations, the 3rd uses 3 operations, ….
1+2+3+… + (n-1) + n = (n(n+1)) / 2 = n2/2 + n/2
This is slightly better than the full nested loop (½ is a constant).
This is slightly better than the full nested loop (½ is a constant).
4. Cubic Function
f(n) = n3
Given an input n, f(n) is equal to n3.
Example:
for()
for()
for()
for()
for()
5. Exponential Function
f(n) = bn
b is the base.
n is the exponent.
f(n) = 2n
Example:
A loop starts with one operation and then doubles the number of operations with each iteration. In the nth iteration, the number of operations is 2n.
1 + 2 + 4 + 8 + … + 2n-1 = 2n - 1
6. Logarithm Function
f(n) = logb n
For some constant b > 1,
x = log bn if and only if bx = n
The most common base in CS is 2:
f(n) = log n
220 = 1,048,576
Log21048576 = 20
Example:
Binary search is very fast with logarithm function.
If we use the binary search method to search a desired key in an array of 1,048,576 elements, it takes about 20 iterations.
7. N-Log-N Function
f(n) = n log n
Example:
Quick sort's average performance belongs to this function. It is much faster than Selection Sort.
If we use the quick sort method to sort an array of 1,048,576 elements, it takes about 20 * 1,048,576 iterations.
Comparing Growth Rates
Algorithms with running time proportional to the constant or logarithm function – ideal.Algorithms with running time proportional to the linear or N-logN function – very good.
Algorithms with running time proportional to quadratic or cubic function – less practical, but still feasible for reasonably small input sizes.
Exponential function is infeasible for all but the smallest sized inputs.
Ranking
| Constant | Log N | N | N-logN | N2 | N3 | 2N |
|---|---|---|---|---|---|---|
| 20 | Log 5000000 | 8N + 100 | 5N Log N + 500 | 3N2 + 20N | N3 + 2N2 + 4N | 230 |
Big O Notation
Asymptotic Notations:Big-Oh [ O ], Big-Omega [ Ω ], Big-Theta [ Θ ]
O-notation
Two functions f(n) and g(n) are defined on all positive integers to real numbers.
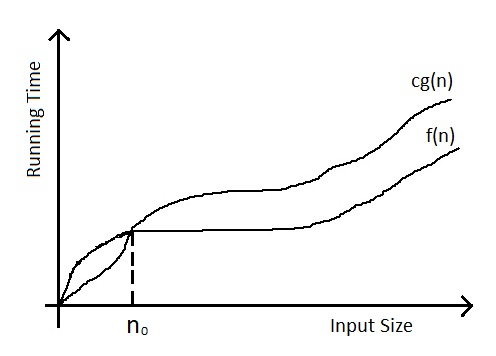
f(n) = O(g(n))
if there exists a positive constant c and n0
such that (∃) 0 <= f(n) <= cg(n) for all n >= n0
if there exists a positive constant c and n0
such that (∃) 0 <= f(n) <= cg(n) for all n >= n0
Examples:
1) 8n –2 = O(n)
Let's prove 0 <= 8n - 2 <= cn
To prove, we need to find c > 0 and n0 > 0
∃ (such that) 8n – 2 <= cn
∀ (for all) n >= n0
Take n0 = 1 and c = 8, 0 <= 8n - 2 <= 8n
It is true because any real number >= 8 will work for c,
and any integer >= 1 will work for n0.
It is true because any real number >= 8 will work for c,
and any integer >= 1 will work for n0.
2) 5n2 – 6n = O(n2)
Let's prove 0 <= 5n2 – 6n <= cn2
Take c =5, n0 = 2, it is true for all n >= n0
3) 3n2 + 4n + 2 = O(n2)
Let's prove 0 <= 3n2 + 4n + 2 <= cn2
Take c = 4
| n0 | 3n2 + 4n + 2 | <= | cn2 | True or False |
|---|---|---|---|---|
| n0 = 1 | 3 * 1 + 4 * 1 + 2 = 10 | <= | 4 * 1 = 4 | Not true |
| n0 = 2 | 3 * 4 + 4 * 2 + 2 = 22 | <= | 4 * 4 = 16 | Not true |
| n0 = 3 | 3 * 9 + 4 * 3 + 2 = 41 | <= | 4 * 9 = 36 | Not true |
| n0 = 4 | 3 * 16 + 4 * 4 + 2 = 66 | <= | 4 * 16 = 64 | Not true |
| n0 = 5 | 3 * 25 + 4 * 5 + 2 = 97 | <= | 4 * 25 = 100 | True |
At this point, we proved that 3n2 + 4n + 2 = O(n2), when c = 4 and for all n >= 5.
Big O notation allows us to say that f(n) is “less than or equal to” g(n) up to a constant factor and in the asymptotic sense as n grows toward infinity.
f(n) grows at a rate that is “less than or equal to” g(n).
Using O-notation, we can describe the running time of an algorithm merely by inspecting the algorithm’s overall structure.
It is used to characterize running times and space bounds in terms of the size n.
It gives an upper bound on a function, to within a constant factor.
We use it to bound the worst-case running time of an algorithm.
Case Studies
| Algorithms | Performance Running Time in Big O Notation (Time Complexity) |
In-Place |
|---|---|---|
| Sequential Search | O(N) | Yes |
| Binary Search | O(LogN) | Yes |
| Quick Sort | O(NLogN) | Yes |
| Merge Sort | O(NLogN) | No (Require additional memory) |
| Selection Sort | O(N2) | Yes |
| Bubble Sort | O(N2) | Yes |
| Insertion Sort | O(N2) | Yes |
Sequential Search
O(N)
In the worst case, it searches the entire array with N iterations.
In the worst case, it searches the entire array with N iterations.
Binary Search
O(LogN)
The basic step in binary search is to split the array, compare X to the middle element, and then select the half of the array in which to continue the search.
Each basic step reduces the size of the array to half the previous size.
If the array has size N, binary search will require no more than log N basic steps in the worst case.
Binary Search is very efficient. Large increases in the size of the array require very small increases in the number of basic steps, approximately:
The basic step in binary search is to split the array, compare X to the middle element, and then select the half of the array in which to continue the search.
Each basic step reduces the size of the array to half the previous size.
If the array has size N, binary search will require no more than log N basic steps in the worst case.
Binary Search is very efficient. Large increases in the size of the array require very small increases in the number of basic steps, approximately:
| N | Log2N |
|---|---|
| 8 | 3 |
| 32,768 | 15 |
| 1,048,576 | 20 |
Selection Sort
O(N2)
Outer Loop i = 1 n-1 iterations in the inner loop
Outer Loop i = 2 n-2 iterations in the inner loop
......
T(n) = 1 + 2 + 3 + … + n-1
T(n) = 1 + 2 + 3 + … + n-1 + n – n = (n(n+1))/2 – n
T(n) = O(n2)
Quick SortOuter Loop i = 1 n-1 iterations in the inner loop
Outer Loop i = 2 n-2 iterations in the inner loop
......
T(n) = 1 + 2 + 3 + … + n-1
T(n) = 1 + 2 + 3 + … + n-1 + n – n = (n(n+1))/2 – n
T(n) = O(n2)
Average behavior of quick-sort: O(N LogN)
Ideal case: O(N LogN)
An array of size n is partitioned into 2 pieces of size n/2 each.
T(n) = cn + 2T(n/2)
O(N LogN)
The pivot is the key.
We want the pivot to divide the array almost equally.
Randomized quick-sort
The goal of the partition is to divide the array almost equally.
The pivot is a random element of the array.
O(N LogN)
Special Case:
Apply partition() to an array of size n requires O(n) comparisons [Move i and j at least n iterations, at most 2n iterations]
Apply quick-sort to an sorted array requires:
n + (n-1) + (n-2) + … + 1 comparisons
So, it takes O(n2) running time.
Ideal case: O(N LogN)
An array of size n is partitioned into 2 pieces of size n/2 each.
T(n) = cn + 2T(n/2)
O(N LogN)
The pivot is the key.
We want the pivot to divide the array almost equally.
Randomized quick-sort
The goal of the partition is to divide the array almost equally.
The pivot is a random element of the array.
O(N LogN)
Special Case:
Apply partition() to an array of size n requires O(n) comparisons [Move i and j at least n iterations, at most 2n iterations]
Apply quick-sort to an sorted array requires:
n + (n-1) + (n-2) + … + 1 comparisons
So, it takes O(n2) running time.