Sorting and Searching Algorithms
In this section, we study sorting and searching algorithms.
Sorting Concept
Selection Sort
Bubble Sort
Insertion Sort
Quick Sort
Searching Concept
Sequential Search (Linear Search)
Binary Search
Comparable Objects
Sorting Concept
Sorting is a process to rearrange data into some order.Examples:
Sort a list of products by price in descending order (highest to lowest)
Sort a list of students by last name in ascending order (A-Z)
Algorithm comparisonSort a list of students by last name in ascending order (A-Z)
| Sorting Algorithm | Performance Running Time in Big O Notation (Time Complexity) |
Degree of Difficulty | In-Place |
|---|---|---|---|
| Selection Sort * | Slow O(N2) | Simple | Yes |
| Bubble Sort | Slow O(N2) | Simple | Yes |
| Insertion Sort | Slow O(N2) | Not Simple | Yes |
| Quick Sort * | Fast O(NLogN) | Difficult | Yes |
| Merge Sort | Fast O(NLogN) | Difficult | No (Require additional memory) |
Selection Sort
Select the smallest remaining element in the array repeatedly.
Find the smallest element in the array.
Exchange it with the element in the first position.
Find the 2nd smallest element.
Exchange it with the element in the 2nd position.
…
The process continues until the entire array is sorted.
Exchange it with the element in the first position.
Find the 2nd smallest element.
Exchange it with the element in the 2nd position.
…
The process continues until the entire array is sorted.
5 7 2 8 9 1
1 7 2 8 9 5
1 2 7 8 9 5
1 2 5 8 9 7
1 2 5 7 9 8
1 2 5 7 8 9
1 7 2 8 9 5
1 2 7 8 9 5
1 2 5 8 9 7
1 2 5 7 9 8
1 2 5 7 8 9
Bubble Sort
Bubble Sort moves the largest entry to the end of the array by comparing and swapping adjacent elements as an index sweeps through the unsorted portion of the array.
15 12 30 48 29 45 19
12 15 30 29 45 19 48
12 15 29 30 19 45 48
12 15 29 19 30 45 48
12 15 19 29 30 45 48
12 15 30 29 45 19 48
12 15 29 30 19 45 48
12 15 29 19 30 45 48
12 15 19 29 30 45 48
Insertion Sort
Similar to sort a handful of cards in order.
Start with an empty left hand and cards face down on the table.
Remove one card at a time and insert it into the correct position.
To find the correct position, compare the card with each of the cards already in the hand, from right to left.
Remove one card at a time and insert it into the correct position.
To find the correct position, compare the card with each of the cards already in the hand, from right to left.
5 2 4 6 1 3
2 5 4 6 1 3
2 4 5 6 1 3
2 4 5 6 1 3
1 2 4 5 6 3
1 2 3 4 5 6
2 5 4 6 1 3
2 4 5 6 1 3
2 4 5 6 1 3
1 2 4 5 6 3
1 2 3 4 5 6
Quick Sort
Quick Sort is based on the divide-and-conquer algorithmic design pattern.
Let's use the following array to demonstrate the quick sort algorithm.
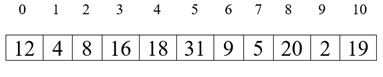
A is an unsorted array.
p = 0 The left-most index of A
r = 10 The right-most index of A
x = A[p] = A[0] = 12 pivot
i = p – 1 = 0 – 1 = -1
j = r + 1 = 10 + 1 = 11
p = 0 The left-most index of A
r = 10 The right-most index of A
x = A[p] = A[0] = 12 pivot
i = p – 1 = 0 – 1 = -1
j = r + 1 = 10 + 1 = 11
The quick sort key component is the Partition(A, p, r) method.
The following images show how the method works.

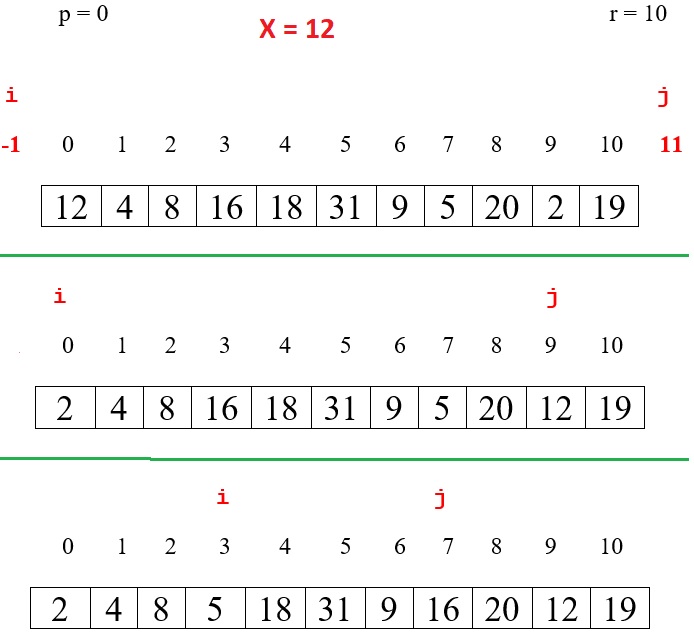
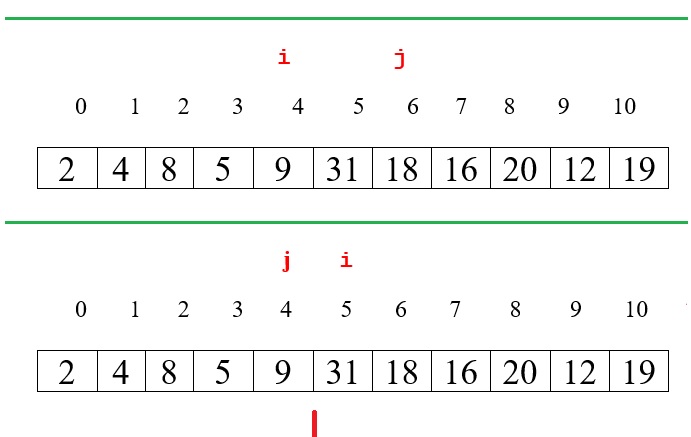
The Partition() method created a partition at index j:
elements on the left <= x (pivot)
elements on the right >= x (pivot)
elements on the right >= x (pivot)
To sort the array, call partition method recursively on the left and right sub-arrays until only one element remaining. Then the entire array is sorted.
Another Example: 18 2 9 22 4 35 7 11 15 30 29
Searching Concept
Searching is a process of finding a designated target element within a group of items, or determining that the target does not exist within the group.
The group is the search pool such as an array.
Sequential search
Binary search
Sequential search
Binary search
Sequential Search (Linear Search)
To search an array A[0..N-1] for a value X, start at
the index of one end of the array.
Step index through the array, examining each A[index] to see if it is equal to X.
Stop the process if X is found and return the index.
In the end of the process, if X is not found, return -1.
Step index through the array, examining each A[index] to see if it is equal to X.
Stop the process if X is found and return the index.
In the end of the process, if X is not found, return -1.
Other Examples:
Find the largest or smallest element in the array.
Binary Search
Find the position of a search key, k, in an ordered array A[] of distinct keys.
It requires the array in sorted order.
If the array is not sorted, the binary search does not work.
The search starts with the element in the middle of the array.
If that element is the desired value, the search is over.
Otherwise, the value in the middle element is either greater or less than the desired value.
If it is greater than the desired value, further search the left half of the array.
Otherwise, further search the right half of the array.
Repeat the process as needed while adjusting the start and the end points of the search.
If the array is not sorted, the binary search does not work.
The search starts with the element in the middle of the array.
If that element is the desired value, the search is over.
Otherwise, the value in the middle element is either greater or less than the desired value.
If it is greater than the desired value, further search the left half of the array.
Otherwise, further search the right half of the array.
Repeat the process as needed while adjusting the start and the end points of the search.
Binary Search Algorithm:
The search starts at the middle of A[] to compare k and A[middle]
middle = (0 + (N-1)) / 2
If k == A[middle],
found it, the search terminates
Else if k < A[middle],
a further search is conducted among the left of A[middle]
Else,
a further search is conducted among the right of A[middle]
By repeatedly halving the size of the search interval, either find it or fail to find it.
middle = (0 + (N-1)) / 2
If k == A[middle],
found it, the search terminates
Else if k < A[middle],
a further search is conducted among the left of A[middle]
Else,
a further search is conducted among the right of A[middle]
By repeatedly halving the size of the search interval, either find it or fail to find it.
Example
Find the number 29 in the following sorted array:
8 15 22 29 36 54 55 61 70 73 88
First, compare 29 to the middle value 54
We now know that if 29 is in the list, it has to be in the left half of the list.
8 15 22 29 3654 55 61 70 73 88
With one comparison, we have eliminated half of the data.
Then compare the desired number to 22, eliminating another quarter of the data.
The same process continues until only one element left in the sub-array.
If the desired number is found, return the index.
Otherwise, return -1 after the process ends.
We now know that if 29 is in the list, it has to be in the left half of the list.
8 15 22 29 36
With one comparison, we have eliminated half of the data.
Then compare the desired number to 22, eliminating another quarter of the data.
The same process continues until only one element left in the sub-array.
If the desired number is found, return the index.
Otherwise, return -1 after the process ends.
Binary search can be done with either recursion or loop.